I nuovi corsi
Corso di geometria.
di Ernesto Fassetta

Se qualcuno non riesce a capire quanto sia semplice la matematica, è soltanto perché non si rende ben conto di quanto sia complicata la vita.

(John von Neumann)


Archimede in un dipinto
di Domenico Fetti.
Immagine estratta dal sito internet:
wikipedia.org/wiki/Archimede.

 

 Normalmente, nell’insegnamento scolastico della matematica, si insegna, e quindi si apprende, come si deve fare per risolvere dei problemi pratici e, generalmente, se ne spiega il perché, quale aspetto più importante dei concetti generalizzati, atti a una valida didattica per la formazione dell’individuo. Ci si dibatte, pertanto, fra meccanismi procedurali, regole, teoremi, formule, numeri fissi, ecc., che seguono il filo logico del ragionamento. La matematica è una disciplina in cui lo svilupparsi della materia e il progredire della conoscenza è affidato esclusivamente al ragionamento logico e al pensiero astratto. Ora, a una certa distanza da quei tempi scolastici, escludendo gli eventuali pochi che per professione o altri motivi abbiano continuato a coltivare questa disciplina, buona parte di tali apprendimenti possono risultare dimenticati o, quanto meno, assopiti in ricordi piuttosto nebulosi. Si propone, perciò, una escursione dimostrativa avente per tema Il cerchio e Pi greco, dalla quale far riaffiorare i vaghi ricordi che portano alla conoscenza, attraverso lo svilupparsi del ragionamento basato su di un processo logico.

Nel cerchio, figura geometrica che prenderemo in esame, sappiamo che esiste un numero strano, quasi misterioso, la cui utilizzazione ci consente di calcolare la lunghezza della circonferenza e l’estensione della superficie. Come si trova la lunghezza della circonferenza del cerchio? Diametro moltiplicato per 3 e 14 (oppure raggio per 6 e 28). E come si calcola l’estensione della sua superficie (o area)? Raggio per raggio per 3 e 14 (o quadrato del raggio per 3,14). Oppure, come si dice con formula e linguaggio più stringato e rigoroso: r2 (Pi greco erre quadrato). Tutto questo, più o meno, lo si ricorda; ma perché bisogna agire in tal modo? Quale è il potere magico di questo numero fisso 3,14 che ci permette di risolvere i due problemi? Certamente non si è mai dubitato della correttezza della procedura, magari assunta dogmaticamente, ma difficilmente si è in grado di afferrarne il significato e quindi il perché.
In matematica esistono delle assunzioni che dichiarano proposizioni semplici e abbastanza ovvie, di facile comprensione, il cui concetto è fornito dall’intuizione, e che si definiscono assiomi ovvero ciò che è evidente per se stesso. Così, per esempio, dalla tipica relazione aristotelica: se A = B e B = C si deduce che A = C. Esistono peraltro assunzioni più complesse, che si definiscono teoremi ovvero ciò che si contempla, i quali sono più difficili da capire e richiedono pertanto una dimostrazione, che deve essere chiara, convincente, veritiera e inconfutabile.

Dopo queste motivazioni e questi presupposti, vediamo ora di approfondire la natura di e di dimostrare il suo coinvolgimento nel cerchio.

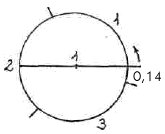è il simbolo matematico che indica il rapporto esistente nel cerchio tra il diametro (considerato 1 unità di misura) e la circonferenza (appunto 3,14 unità della stessa misura). In sostanza, la circonferenza del cerchio è 3,14 volte il diametro. Anticamente, egizi, babilonesi, ebrei e indiani, che praticavano una matematica piuttosto semplice e rudimentale, accontentandosi di valori approssimativi, consideravano questo rapporto 1 a 3. Perfino in Cina, una fra le più antiche civiltà scientifiche e matematiche, i cinesi continuarono a usare nei loro calcoli il valore di 1 a 3 fino al III sec. a.C. I matematici greci precedenti Archimede avevano migliorato il risultato tentando di calcolare la frazione decimale, arrivando a valori come 3,1547, ma ancora imprecisi.

Fu Archimede di Siracusa, uno dei più grandi matematici e fisici di tutti i tempi, che nel III sec. a.C, in terra italica della Magna Grecia, osservando che il perimetro di un poligono inscritto nella circonferenza è minore di tale circonferenza, e il perimetro del poligono circoscritto è invece maggiore, dedusse che la circonferenza doveva essere intermedia. Sviluppando questo pensiero matematicamente con poligoni aventi un numero sempre maggiore di lati, ovvero 12, 24, 48, 96, e confrontandone i perimetri, riuscì a calcolare quasi esattamente il suo valore, che risultò compreso fra 3,1408 e 3,1428 (in realtà è 3,1415...). Con l’affermarsi della geometria greca, si passò dalla ricerca di una regola empirica a uno studio razionale. Ancora più sorprendente di questa precisione fu il fatto che Archimede calcolò questi valori senza l’ausilio di un simbolo per lo zero e senza disporre di alcuna sorta di notazione decimale.

Il famoso rapporto della circonferenza al diametro non ebbe un nome né un simbolo fino al XVII sec; i matematici lo indicavano sempre con perifrasi come: quantitas, in quam cum multiplicetur diameter, proveniet circumferentia (la quantità che, moltiplicata per il diametro, fornisce la circonferenza).

Questo rapporto fisso, invariabile, venne quindi simboleggiato con p, lettera P dell’alfabeto greco, scelta come iniziale del termine greco periphèria, cioè periferia, che sta per circonferenza. I geometri successivi ad Archimede, una interminabile sequela di ciclometristi (da kiklòs mètron, misuratori del cerchio), attraverso i secoli cercarono, senza successo, di trovare il valore esatto di . Tali studi ebbero il solo risultato di stabilire un maggior numero di cifre decimali esatte. Nel XIII sec. i matematici cinesi si spinsero ben oltre Archimede e, considerando un poligono di 3072 lati (un dodecagono raddoppiato 8 volte), pervennero al risultato esatto di 3,141592.

Nel 1770 il matematico svizzero Jean Henri Lambert dimostrò che era impossibile trovare una frazione il cui valore eguagliasse quello di , in quanto p è un numero irrazionale (vale a dire che esprime il rapporto fra due grandezze incommensurabili), rappresentato da un numero decimale illimitato non periodico, che non si può ridurre a forma di frazione. Ciò confermava l’intuizione di Archimede, secondo il quale si poteva conoscere p solo attraverso un procedimento di indefinita approssimazione. Finalmente, nel 1882, il matematico tedesco Carl Ferdinand von Lindemann concluse lo studio di questo millenario problema dimostrando che p è un numero irrazionale trascendente, tale cioè che non esiste alcuna equazione algebrica a coefficienti razionali che lo ammetta come radice.

Dunque = 3,141592653... con cifre decimali interminabili.

Modernamente, con l’aiuto del computer, sono state determinate milioni e milioni di cifre decimali. Oggigiorno, gli ultimi eroi del , con un supercalcolatore, hanno calcolato oltre 50 miliardi di cifre decimali! Nota di cronaca apparsa sulla stampa: Il giapponese Akira Haraguchi, 60 anni, ha recitato centomila decimali che compongono il pi greco, battendo il record del mondo di memorizzazione. E’ avvenuto ieri, 4 ottobre 2006, a Tokyo. L’elenco è durato sedici ore. Il pubblico ha dato i numeri.

Ma tutto ciò ha puro significato teorico, di astratta ricerca matematica, in quanto, in generale, possono bastare i soli quattro decimali archimedei o, eventualmente, l’aggiunta di alcuni altri. In effetti neppure l’ingegnere più maniaco della precisione richiederebbe mai più di 7 decimali di , e neppure un fisico ne userebbe più di 15 o 20. Bastano 10 decimali per calcolare la circonferenza terrestre con un margine d’errore dell’ordine del cm. E 30 decimali sono sufficienti per determinare la circonferenza dell’intero universo visibile, con un margine d’errore non percepibile con il microscopio più potente.

Per calcoli pratici sono sufficienti due decimali. Come si suol dire: = 3,14. E’ possibile una semplice verifica, in modo non perfetto ma utile per rendersene conto: basta prendere un oggetto rotondo (piatto, tazza, vaso, pentola, tagliere...) e misurarne il bordo (circonferenza) con un metro a nastro da sartoria; con un po’ di attenzione misurarne poi il diametro (la massima larghezza, passando per l’ipotetico centro) e confrontare i due valori: moltiplicando per 3,14 la misura del diametro si ottiene la circonferenza o, al contrario, dividendo per 3,14 la circonferenza si ottiene il diametro. Provare per credere!

Per la nostra dimostrazione, del resto, non sarà neanche necessario dare il valore numerico a , basterà usare il suo simbolo nella formulazione algebrica, dove indicheremo c per circonferenza, d per diametro ed r per raggio, e in cui simboli e numeri senza segni di operazioni vanno intesi come prodotti. Come si calcola dunque la circonferenza del cerchio? Semplicemente moltiplicando per il diametro: c = d, oppure c = 2 r (datosi che r = 1/2 d, bisogna raddoppiare p per mantenere l’eguaglianza).

Ora, per ben chiarire l’area o superficie del cerchio, prendiamo in esame la superficie dei poligoni regolari, ovvero di quelle figure geometriche conformate da lati e angoli tutti uguali. Nel triangolo, la superficie (S) di calcola S = b h/2 (base per altezza diviso 2). E’ palese che moltiplicando b per h si ottiene la superficie di un rettangolo doppio del triangolo, pertanto bisogna dividere per 2. Riferiamoci adesso, a titolo di esempio, a un poligono regolare di sei lati: l’esagono. Questo può essere diviso, unendo i vertici con il baricentro (o mediante le 3 diagonali maggiori), in 6 triangoli uguali (nel caso dell’esagono sono equilateri). Per calcolare la superficie si dovrà trovare quella di un triangolo (b h/2) e poi moltiplicare per 6 (i triangoli che coprono l’intera superficie); quindi, S = 6 b h/2.

Sei volte il lato corrisponde al perimetro (p) e l’altezza del singolo triangolo si dice apotema (a) del poligono, perciò l’area assume questa nuova definizione: S = p a/2 (oppure: 1/2 p a, semiprodotto del perimetro per apotema). La superficie è dunque scomponibile in 6 triangoli uguali affiancati e corrisponde a metà dell’area del rettangolo che ha per lati p e a, ed è equivalente a un unico triangolo avente p = b e a = h.


In forza di quanto detto, possiamo adesso dedicarci a comprendere perché la superficie del cerchio è dettata dalla formula r2, il che sta a significare che l’area del cerchio equivale a 3 volte più 14 centesimi l’area del quadrato costruito sul raggio dello stesso cerchio. La somma delle superfici dei 3 quadrati di lato r, più la frazione, equivale alla superficie del cerchio. Ma perché dunque?

Il cerchio, come tutti i poligoni regolari, secondo l’enunciazione archimedea, può essere trasformato in un triangolo equivalente, datosi che il cerchio è da considerarsi un poligono regolare con un numero infinito di lati. Il triangolo equivalente avrà per base una lunghezza pari alla circonferenza rettificata (AB) del cerchio e l’altezza pari al raggio. Pertanto il calcolo sarà: S = c r/2 (circonferenza per raggio diviso 2). Ma la circonferenza, come detto in precedenza, è 2 r quindi, sostituendo la c, avremo 2 r r/2; semplificando (dovendo raddoppiare e poi dividere a metà le due operazioni si annullano), eliminiamo il primo e l’ultimo 2: 2 r/2 abbiamo così ottenuto la formula rr ovvero r2, come volevasi dimostrare.